Your other option is to use blackjack simulators that can calculate the RoR for you. We can distinguish between two types of Risk of Ruin, namely session RoR and the RoR for players' full bankroll. Risk of Ruin is a love story unlike any you've ever read—dark, disturbing, irreverent, some might say sacrilegious—while protagonists Bart and Stacy may be the most compelling misfits to go on the lam since Bonnie and Clyde.
Professionals, who make a living from blackjack, will usually prefer the smallest risk of ruin possible (such as 1% or even less). If a non-professional player uses 5% risk of ruin as an acceptable risk level, in order to size his/her total bankroll and betting units, he/she needs to use the amount of his/her largest bet in the calculation. I was explaining the basics of card counting to a stats guy I know, and he pointed something that really stumped me. I don't get what risk of ruin means, I don't think. If you have any non-zero risk of ruin, and you play long enough, won't you always eventually hit a streak bad enough to wipe you out? In which case, what does it mean to have a 5% risk vs. A 2% risk, if everyone busts.
Blackjack Apprenticeship Risk Of Ruin Death
Betting style:
(martingale)
..
In addition..I would play 'never bust' - always force the dealer to make a hand AND beat mine.
..
First, what are the odds of losing 9 straight hands where you never bust.
The odds of winning with the 'never bust' strategy are approximately equal to the odds of being dealt either a 19-21 or 2-11 and upgrading to 19-21, plus the odds of dealer busting. You will win approximately 40% of hands and lose about 50%. Pushes not counting, you will lose about 55% of hands and win 45%.

Blackjack Apprenticeship Risk Of Ruin Wisdom
edit: Nevermind the formula. I've been told this calculation for the risk of a losing streak is oversimplified, and seems to double-count longer streaks. An accurate calculator can be found here: http://www.pulcinientertainment.com/info/Streak-Calculator-enter.html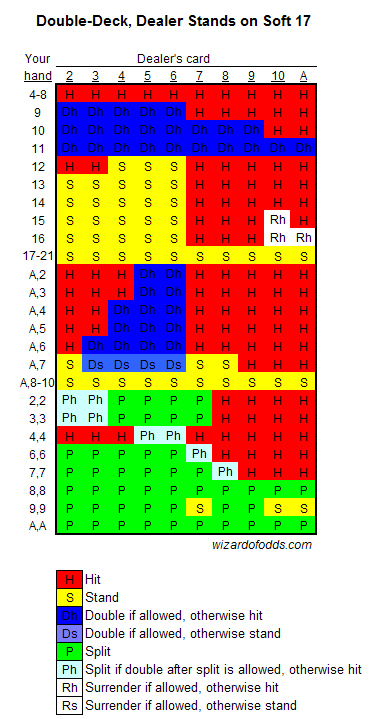
---
However, this should be put into context for comparing with other betting patterns. Here is a post I recently wrote elsewhere about martingale, I'll repost it here, tweaked a bit for context.
---
While most betting systems are mathematically neutral, martingale stands out as being mathematically damaging to the player in all long-term performance metrics, such as risk of ruin, SCORE, time to double the bankroll, and, critically, chance to double the bankroll.
For instance, the risk of ruin in typical blackjack with a 64-bet bankroll is 10% in 1,000 hands, 1.8% in 500 hands, or 0.01% in 200 hands. A 6-step martingaler will run out of his 64 bets the first 6-loss streak he gets. The probability of a 6-loss streak in fair coin flip is 1/64 (or 1/45 in blackjack), and a streak can begin on any hand.
So, it will take only 50 fair coin flips or 36 hands of blackjack to provide a 50% risk of ruin with 6-step martingale. A 10% risk of ruin is reached in a mere 10 hands. A 1.8% chance will be exceeded in just 6 hands, since your first 6-hand sequence entails a 2.2% risk of ruin. That is for a bankroll that will last flat-bettors through thousands of hands.
All this while, martingale limits the winnings to a single unit at a time, slowing down the winnings. Even under ideal conditions, perfect 1-0-1 (just what martingale is designed for), a 6-step martingaler needs 128 bets to double his bankroll, a 86% risk or ruin in coin flip or 94% in blackjack.
So while per-bet house edge is unchanged, with a martingale the chance to double a 64-bet bankroll is a mere 14% in fair coin flip, as opposed to 50% for a flat-bettor. This is a mathematical disadvantage, voluntarily creating house edge even in a game that doesn't have any. All martingale provides in the long run is just massively increased risk of ruin, without a corresponding increase in gain.
---
Or keep schtum.
Your ire can be reserved for the point when the poster has revealed themselves to be willfilly ignorant/selling snake oil/unable to follow a logical train of thought.
Both questions could have been answered with some math, and it might just have been that the math would have been enough to convince the OP why it's a bad idea (TM).
As with all forum, what's old too one person is brand new to another, and repeated questions and themes will always appear. Or the forum disappears up its own backside into a insular community of anti-social jackarsery.
Well, you did offer some pretty ridiculous advice--'wait until the table gets hot.' Anyone offering such advice might very well have to be reminded that there is no such thing as a 'hot table', in the meaning of 'the players have recently won, so the players are more likely to win in the immediate future.'
Yeah - I didn't say 'wait until the table gets hot' or anything of the sort. I said that I've never seen a person make 12 passes in a row. I also said that while it is possible, in my 40 plus years of playing craps I've never seen it. Of course the dice don't remember but craps is a very simple, binary game. It is biased to the dark side. Even the house edge shows that. (And although people scoff at small biases I do not. Small errors accumulate into large errors, small advantages accumulate into large advantages. And even if that advantage is on the losing side I will lose less if I play the don't. That is just a cold, hard mathematical fact).
I also said that I have never seen more than 8 field numbers rolled in a row and while I am certain that it has happened I am also certain that it doesn't happen very often. I am also certain that for every set containing 8 field numbers rolled in a row there has been at least one set of 7.n non-field numbers rolled in a row (there being fewer non-field numbers than field numbers). I am also certain that craps is a closed system and that it contains a small number of events and that it regresses to the mean a lot more often than many people credit it with doing.
So if you are going to quote me try actually reading what I say and quoting me accurately. I think I have had the EV Knighthood up to my ass and beyond and I should be doing better things with my life. So if you will pardon me I will leave you now - for good.
Both questions could have been answered with some math, and it might just have been that the math would have been enough to convince the OP why it's a bad idea (TM).
But why should anyone bother to do the math? It's like resorting to a detailed explication of physics and chemistry to show someone why their scheme to turn cotton balls into plutonium won't work.
It's a far better service to simply say to such a person, 'It won't work.' If you explain the math, and by some miracle that person understands that math and agrees with the conclusion, they'll just go back to their basement and cook up some different system in the forlorn hope that the math will validate that new one.
I think the odds of the math convincing the OP that Martingales don't work were about 40,000,000 to one. I respect the various quixotic tries to do so, though.
OK, I'll answer your question strictly in terms of math.
The odds of winning with the 'never bust' strategy are approximately equal to the odds of being dealt either a 19-21 or 2-11 and upgrading to 19-21, plus the odds of dealer busting. You will win approximately 40% of hands and lose about 50%. Pushes not counting, you will lose about 55% of hands and win 45%.
The odds of losing 9 hands in a row are 0.55^9=1/217. The probability of a 9-hand losing streak is 21% in 60 hands, 40% in 120 hands, 54% in 180 hands, 65% in 240 hands, 90% in 500 hands, 99% in 1,000 hands. The formula is 1-(1-1/217)^(N-8), where N is the number of hands played.
---
However, this should be put into context for comparing with other betting patterns. Here is a post I recently wrote elsewhere about martingale, I'll repost it here, tweaked a bit for context.
---
While most betting systems are mathematically neutral, martingale stands out as being mathematically damaging to the player in all long-term performance metrics, such as risk of ruin, SCORE, time to double the bankroll, and, critically, chance to double the bankroll.
For instance, the risk of ruin in typical blackjack with a 64-bet bankroll is 10% in 1,000 hands, 1.8% in 500 hands, or 0.01% in 200 hands. A 6-step martingaler will run out of his 64 bets the first 6-loss streak he gets. The probability of a 6-loss streak in fair coin flip is 1/64 (or 1/45 in blackjack), and a streak can begin on any hand.
So, it will take only 50 fair coin flips or 36 hands of blackjack to provide a 50% risk of ruin with 6-step martingale. A 10% risk of ruin is reached in a mere 10 hands. A 1.8% chance will be exceeded in just 6 hands, since your first 6-hand sequence entails a 2.2% risk of ruin. That is for a bankroll that will last flat-bettors through thousands of hands.
All this while, martingale limits the winnings to a single unit at a time, slowing down the winnings. Even under ideal conditions, perfect 1-0-1 (just what martingale is designed for), a 6-step martingaler needs 128 bets to double his bankroll, a 86% risk or ruin in coin flip or 94% in blackjack.
So while per-bet house edge is unchanged, with a martingale the chance to double a 64-bet bankroll is a mere 14% in fair coin flip, as opposed to 50% for a flat-bettor. This is a mathematical disadvantage, voluntarily creating house edge even in a game that doesn't have any. All martingale provides in the long run is just massively increased risk of ruin, without a corresponding increase in gain.
---
nice post
Of course - how ignorant of me to forget that single, most important aspect. Oh thank you wise one for setting me on the path to enlightenment.
Blackjack Apprenticeship Risk Of Ruin Wisdom
edit: Nevermind the formula. I've been told this calculation for the risk of a losing streak is oversimplified, and seems to double-count longer streaks. An accurate calculator can be found here: http://www.pulcinientertainment.com/info/Streak-Calculator-enter.htmlThe correct probabilities are 10.6% in 60 hands, 21% in 120, 39% in 240, 65% in 500 and 88% in 1,000 hands.
---
However, this should be put into context for comparing with other betting patterns. Here is a post I recently wrote elsewhere about martingale, I'll repost it here, tweaked a bit for context.
---
While most betting systems are mathematically neutral, martingale stands out as being mathematically damaging to the player in all long-term performance metrics, such as risk of ruin, SCORE, time to double the bankroll, and, critically, chance to double the bankroll.
For instance, the risk of ruin in typical blackjack with a 64-bet bankroll is 10% in 1,000 hands, 1.8% in 500 hands, or 0.01% in 200 hands. A 6-step martingaler will run out of his 64 bets the first 6-loss streak he gets. The probability of a 6-loss streak in fair coin flip is 1/64 (or 1/45 in blackjack), and a streak can begin on any hand.
So, it will take only 50 fair coin flips or 36 hands of blackjack to provide a 50% risk of ruin with 6-step martingale. A 10% risk of ruin is reached in a mere 10 hands. A 1.8% chance will be exceeded in just 6 hands, since your first 6-hand sequence entails a 2.2% risk of ruin. That is for a bankroll that will last flat-bettors through thousands of hands.
All this while, martingale limits the winnings to a single unit at a time, slowing down the winnings. Even under ideal conditions, perfect 1-0-1 (just what martingale is designed for), a 6-step martingaler needs 128 bets to double his bankroll, a 86% risk or ruin in coin flip or 94% in blackjack.
So while per-bet house edge is unchanged, with a martingale the chance to double a 64-bet bankroll is a mere 14% in fair coin flip, as opposed to 50% for a flat-bettor. This is a mathematical disadvantage, voluntarily creating house edge even in a game that doesn't have any. All martingale provides in the long run is just massively increased risk of ruin, without a corresponding increase in gain.
---
Or keep schtum.
Your ire can be reserved for the point when the poster has revealed themselves to be willfilly ignorant/selling snake oil/unable to follow a logical train of thought.
Both questions could have been answered with some math, and it might just have been that the math would have been enough to convince the OP why it's a bad idea (TM).
As with all forum, what's old too one person is brand new to another, and repeated questions and themes will always appear. Or the forum disappears up its own backside into a insular community of anti-social jackarsery.
Well, you did offer some pretty ridiculous advice--'wait until the table gets hot.' Anyone offering such advice might very well have to be reminded that there is no such thing as a 'hot table', in the meaning of 'the players have recently won, so the players are more likely to win in the immediate future.'
Yeah - I didn't say 'wait until the table gets hot' or anything of the sort. I said that I've never seen a person make 12 passes in a row. I also said that while it is possible, in my 40 plus years of playing craps I've never seen it. Of course the dice don't remember but craps is a very simple, binary game. It is biased to the dark side. Even the house edge shows that. (And although people scoff at small biases I do not. Small errors accumulate into large errors, small advantages accumulate into large advantages. And even if that advantage is on the losing side I will lose less if I play the don't. That is just a cold, hard mathematical fact).
I also said that I have never seen more than 8 field numbers rolled in a row and while I am certain that it has happened I am also certain that it doesn't happen very often. I am also certain that for every set containing 8 field numbers rolled in a row there has been at least one set of 7.n non-field numbers rolled in a row (there being fewer non-field numbers than field numbers). I am also certain that craps is a closed system and that it contains a small number of events and that it regresses to the mean a lot more often than many people credit it with doing.
So if you are going to quote me try actually reading what I say and quoting me accurately. I think I have had the EV Knighthood up to my ass and beyond and I should be doing better things with my life. So if you will pardon me I will leave you now - for good.
Both questions could have been answered with some math, and it might just have been that the math would have been enough to convince the OP why it's a bad idea (TM).
But why should anyone bother to do the math? It's like resorting to a detailed explication of physics and chemistry to show someone why their scheme to turn cotton balls into plutonium won't work.
It's a far better service to simply say to such a person, 'It won't work.' If you explain the math, and by some miracle that person understands that math and agrees with the conclusion, they'll just go back to their basement and cook up some different system in the forlorn hope that the math will validate that new one.
I think the odds of the math convincing the OP that Martingales don't work were about 40,000,000 to one. I respect the various quixotic tries to do so, though.
OK, I'll answer your question strictly in terms of math.
The odds of winning with the 'never bust' strategy are approximately equal to the odds of being dealt either a 19-21 or 2-11 and upgrading to 19-21, plus the odds of dealer busting. You will win approximately 40% of hands and lose about 50%. Pushes not counting, you will lose about 55% of hands and win 45%.
The odds of losing 9 hands in a row are 0.55^9=1/217. The probability of a 9-hand losing streak is 21% in 60 hands, 40% in 120 hands, 54% in 180 hands, 65% in 240 hands, 90% in 500 hands, 99% in 1,000 hands. The formula is 1-(1-1/217)^(N-8), where N is the number of hands played.
---
However, this should be put into context for comparing with other betting patterns. Here is a post I recently wrote elsewhere about martingale, I'll repost it here, tweaked a bit for context.
---
While most betting systems are mathematically neutral, martingale stands out as being mathematically damaging to the player in all long-term performance metrics, such as risk of ruin, SCORE, time to double the bankroll, and, critically, chance to double the bankroll.
For instance, the risk of ruin in typical blackjack with a 64-bet bankroll is 10% in 1,000 hands, 1.8% in 500 hands, or 0.01% in 200 hands. A 6-step martingaler will run out of his 64 bets the first 6-loss streak he gets. The probability of a 6-loss streak in fair coin flip is 1/64 (or 1/45 in blackjack), and a streak can begin on any hand.
So, it will take only 50 fair coin flips or 36 hands of blackjack to provide a 50% risk of ruin with 6-step martingale. A 10% risk of ruin is reached in a mere 10 hands. A 1.8% chance will be exceeded in just 6 hands, since your first 6-hand sequence entails a 2.2% risk of ruin. That is for a bankroll that will last flat-bettors through thousands of hands.
All this while, martingale limits the winnings to a single unit at a time, slowing down the winnings. Even under ideal conditions, perfect 1-0-1 (just what martingale is designed for), a 6-step martingaler needs 128 bets to double his bankroll, a 86% risk or ruin in coin flip or 94% in blackjack.
So while per-bet house edge is unchanged, with a martingale the chance to double a 64-bet bankroll is a mere 14% in fair coin flip, as opposed to 50% for a flat-bettor. This is a mathematical disadvantage, voluntarily creating house edge even in a game that doesn't have any. All martingale provides in the long run is just massively increased risk of ruin, without a corresponding increase in gain.
---
nice post
Of course - how ignorant of me to forget that single, most important aspect. Oh thank you wise one for setting me on the path to enlightenment.
What did I do?
But why should anyone bother to do the math?
It's a far better service to simply say to such a person, 'It won't work.' If you explain the math, and by some miracle that person understands that math and agrees with the conclusion, they'll just go back to their basement and cook up some different system in the forlorn hope that the math will validate that new one. Island lake casino harris mi.
I disagree with your comments for two reasons. I think that the reason this website exists is to educate and inform people. By just telling someone something won't work in answer to their question..
So what I can't get my mind around basically is..
First, what are the odds of losing 9 straight hands where you never bust.
Second, since extra profit will be made whenever I get a blackjack (and obviously, the farther into the sequence I am, the higher the profit), how significant is that to the overall final edge?
Any input would be greatly appreciated! I tested this method out on a free game online for around 3 hours (I know, small sample size for sure) and profited $435.
.. you are in effect telling them that their question is not valid and is not worth answering. I assume that you have decided that the question is not worth answering mathematically mkl but please don't presume that others on this site feel the same way. I know you like to respond to every post on the site (or at least the overwhelming evidence points to that conclusion) but perhaps you might look at a post such as this one and simply decide not to post anything instead of jumping on it and insulting the poster.
I know (as does anyone who has read your posts) that you don't believe any kind of Martingale system can possibly create an advantage for a player. I agree with you as do most here. If you feel you've explained this to death and have no inclination to take the time to explain it again, you could just ignore the question.
My second point is that having read your posts in the past it seems to me that you are not sufficiently capable of actually performing the math to answer many of these math oriented questions. It's not that you can't add and subtract and multiply and divide; I'm sure you can. It just seems that the breaking down of the questions to be able to create a workable formula is a bit over your head from time to time. Rather than leave the question for someone better suited to provide an answer, you prefer to give some half-hearted quasi-mathematical answer and then deride the person who has asked the question.
I'd say that's what's happened here.
Blackjack Apprenticeship Practice
To the OP (Bruski), I'm working on an answer.Some blackjack players are so preoccupied with mastering perfect basic strategy and card counting that they neglect their money management. In blackjack, just like in any other casino-banked game, managing one's bankroll adequately is of great significance.
Having said that, we would also like to point out bankroll management is powerless when it comes to decreasing the house edge. What it does help with is longevity, or preserving your blackjack bankroll for a longer period of time. No matter how perfect your play is, you are guaranteed to lose your money without discipline and proper bankroll management.
Building a Bankroll – How Much Money Do You Need to Play Blackjack?
Let's start by specifying that your bankroll is the money you have set aside strictly for the purpose of playing blackjack. We suspect you already know this but just to play it safe, we shall say it again – you should never use money you need to cover your day-to-day expenses for playing blackjack, regardless of your level of skill or previous experience.
Our advice is to place your blackjack bankroll in a separate account and withdraw from it when you plan to attack the blackjack tables. Once you finish with the assault, you go back and deposit whatever you have left alongside any winnings you have generated during the session.
You should leave your bankroll alone in the beginning and avoid using it for any non-blackjack-related purchases. Once you succeed in building your bankroll, you can reward yourself by buying something with some of the winnings you have generated.
Table Limits and Session Bankrolls
With this clarification out of the way, we warn you there is no uniform bankroll size that applies to absolutely all blackjack players. The edge skilled players get inevitably manifests itself over the long term. Anything can happen over the course of a single session, a week, or even a few months.
Experiencing short-term losses, even if you are an accurate card counter, is hardly anything unheard of. The bottom line is as a serious blackjack player, you need a bankroll that is large enough to withstand the losses you may incur on a short timescale.
The overall amount you allocate for blackjack play should be broken down into smaller session bankrolls. How much you allocate for a single session is closely linked to what table limits you play.
If there are lots of casinos in your area but you have limited funds for blackjack play at your disposal, the smartest thing to do is scout the different gambling halls and find a table with low enough limits to accommodate your small bankroll. Provided that there is a single casino with high limits in your city, you better wait until you save a sufficiently large bankroll to play such stakes.
Show MoreHide MoreA session bankroll should be at least 50 times the lowest bet at the table. This is the bare minimum, recommended for basic strategy players and flat bettors. Respectively, players who count cards and move their bets with the true count are recommended to put aside at least 100 times their top bets.Thus, if there are $10 tables in your vicinity and you flat bet at this minimum with basic strategy, your session's bankroll should be at least $500. Your max bet should not exceed the amount of $10 under any circumstances. Provided that you are a novice card counter who uses a less aggressive bet spread like 1 to 5, you will need a session bankroll of at least $5,000.
Each number 1 through 5 corresponds to the number of base bets you need to wager when you move with the true count. You put out 5 units or $50 on a count of +5 or higher, 4 units or $40 on a count of +4, and so on. One unit of $10 is wagered on a count of +1 as well as on neutral and negative counts.
Evaluating Your Risk of Ruin
Disciplined players who exercise good money management are well-acquainted with the term 'Risk of Ruin', abbreviated as RoR. For those of you who are not, RoR denotes the probability of a given player losing their entire bankroll.
There are several values you need to take into account when estimating your Risk of Ruin, including your standard deviation, your bankroll in units, and your win rate per every hundred hands. There are free RoR calculators on the web players can use to accurately estimate the likelihood of busting their full bankrolls. Your other option is to use blackjack simulators that can calculate the RoR for you.
We can distinguish between two types of Risk of Ruin, namely session RoR and the RoR for players' full bankroll. The former denotes the likelihood of the player losing their entire bankroll for the session while the latter shows you the probability of busting your overall lifetime bankroll.
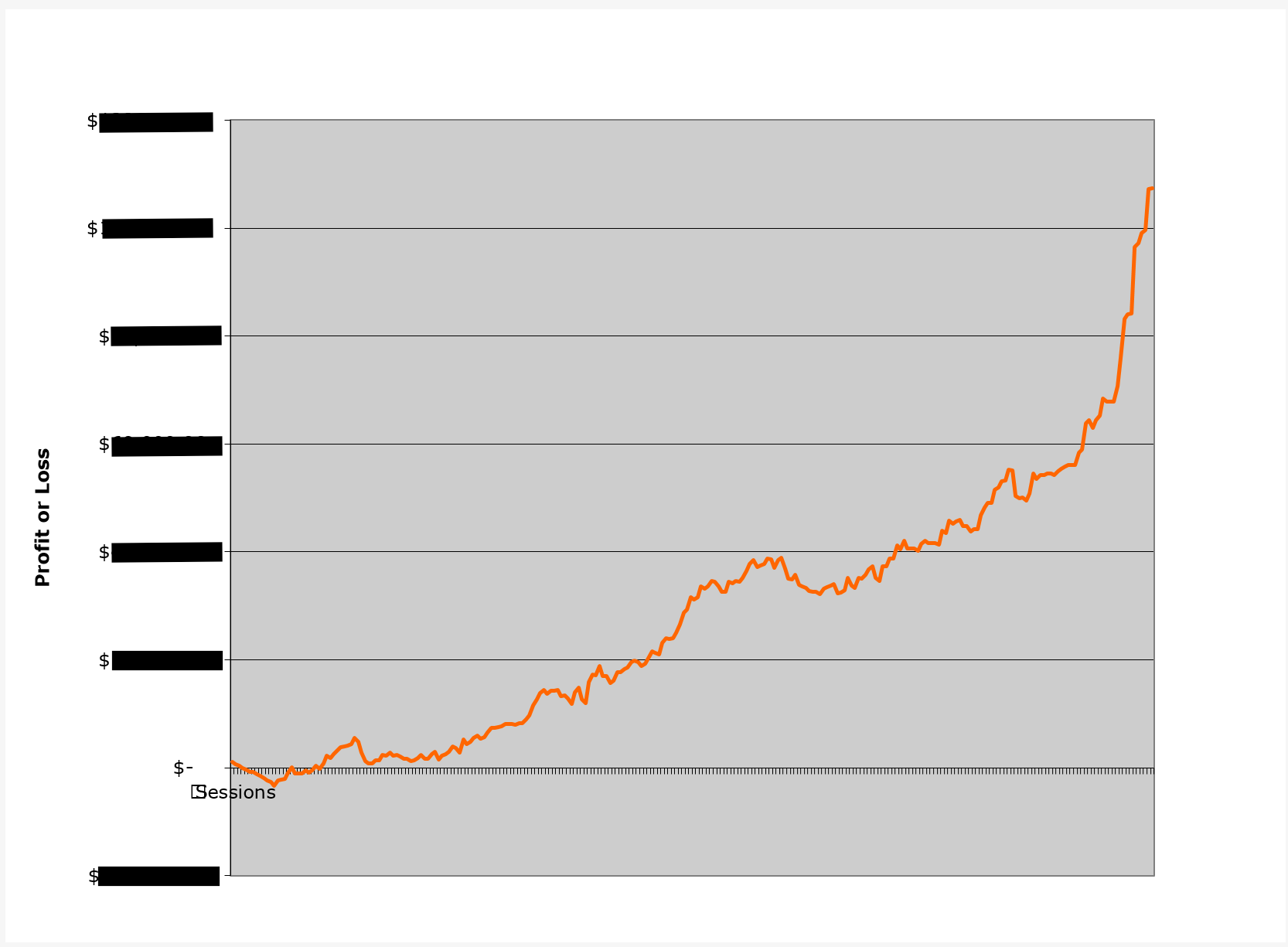
To give you an example, let's suppose you have a session bankroll of $2,000, play perfect basic strategy, and flat bet $10 per hand. You have 200 base betting units at your disposal. The software you are using has calculated that you have a session RoR of 18%.
This means that eventually you will end up losing your $2,000 around 18% of the time. And the opposite, your bankroll will increase 82% of the time. Meanwhile, if you cut your bankroll in half to $1,000, or 100 units, your RoR will jump to nearly 32%, which exceeds the tolerable limits. In the other 68% of the time, you will increase the bankroll.
It is important to specify that different players are willing to put up with different RoR percentages. At the end of the day, this is all a matter of individual tolerance. The bottom line is the bigger your bankroll is and the more base betting units you have, the lower your RoR will be.
Understanding Standard Deviation
The term standard deviation (SD) is normally used in mathematical statistics in relation to the distribution of expected results. In blackjack, it denotes the distribution of players' results within a range of probable outcomes.
It tells you how frequently a specific outcome will deviate from your expected average. This is important because it enables you to assess whether you are playing a losing or a winning game as well as to decide how big your bankroll should be for any given session.
It is unrealistic to think you can win each and every blackjack session, even if you are perfect at basic strategy and count cards with great accuracy. A low standard deviation indicates the actual results fall closely within one's expectations.
We shall explain how standard deviation works with a simple coin-flipping example. A coin has a 50% chance of landing on tails and a 50% chance of landing on heads. Yet, you cannot expect the coin to land precisely 50 times on tails and 50 times on heads in every 100 trials, or at least not in the short term. Sometimes it may land only 45 times on tails and 55 times on heads which happens roughly 2/3 of the time or around 68.3%.
Show MoreHide MoreIn the context of blackjack, the standard deviation of a single hand you play in a six-deck game is estimated at 1.14. Thus, you are expected to win or lose roughly 1.14 bet units around 68.3% of the time within one standard deviation, 2.28 betting units will be lost/won 95% of the time within two standard deviations and 3.42 units will be lost/won 99.7% of the time within three standard deviations. The distribution of these results is shown on the so-called Gaussian bell-curves.Knowing their standard deviation enables players to calculate the probability of winning or losing a given number of units over the course of a certain number of hands. You do this by multiplying your standard deviation by the square root of the number of hands you play.
So if your sample size involves 400 hands with a standard deviation of 1.14, you can expect to lose or win √400 x 1.14 = 20 x 1.14 = 22.8 betting units around 68.3% of the time. Respectively, 95% of the time, you can expect results within two standard deviations where you will lose √400 x 2.28 = 20 x 2.28 = 45.6 betting units over the course of 400 hands. And finally within three standard deviations, you will lose √400 x 3.42 = 20 x 3.42 = 68.4 betting units every 400 hands 99.7% of the time.
Standard deviation may be complex to understand if you are a novice but is nevertheless of great importance. You need it when calculating your RoR, which in turn helps you determine the bankroll you need. Do not be intimidated, however, as you can figure out what your RoR is by using a simulator software Online roulette free sign up bonus no deposit. or one of the online RoR calculators.
House Edge and Hourly Losses
The beauty of using basic strategy is that it reduces the house edge in blackjack to such an extent that you are nearly playing a break-even game. Yet, basic strategy is not powerful enough to completely overcome the built-in casino advantage.
Even if you are perfect at basic strategy, the house edge will inevitably cause a dent in your blackjack bankroll over the long run. This dent, however, will be far more significant if you rely on gut feelings and hunches instead of using the optimal strategy.
Knowing the house edge of a blackjack game helps you calculate the hourly losses you can expect to incur in the long term. Suppose you choose a table with more liberal rules like those offered across Las Vegas Strip casinos where the house edge revolves around 0.36%.
You multiply this percentage by the average number of hands you play per hour and your average bet size. Assuming you are a recreational player who joins mostly full tables and bets $30 per hand on average, you will be able to go through roughly 80 hands per hour.
Therefore, the long-term hourly losses you can expect to see will amount to ($30 x 80 hands x 0.36)/100 = 864/100 = $8.64.You will inevitably arrive at this figure when you get enough playing hours under your belt. By 'enough', we mean tens of thousands of hours as anything can happen in the short run.
Unlike basic strategy players who are practically betting on a negative EV game, skilled and disciplined card counters are able to overcome the house edge. They have an advantage of around 1% at six-deck games with decent rules.
This enables them to grow their bankrolls overtime instead of incurring long-term losses. They calculate their expected hourly winnings with the same formula, i.e. by multiplying their edge by the average bet size and the number of hands they play per hour.
Respectively, an accurate counter who plays heads-up at an empty table with at a 1% advantage and goes through 100 bets of $30 per hour can expect long-term hourly returns of ($30 x 100 hands x 1)/100 = 3,000 / 100 = $30.
Handling Losing Sessions
Variance is inherent to all casino games, including blackjack. All players, no matter how skilled they are, will inevitably end up going through some losing sessions. Knowing how to handle these and when to call it quits is of great significance for preserving your bankroll.
Needless to say, chasing your losses is a terrible idea. The rule of thumb all smart blackjack players should follow is to always leave a table before they have busted their entire session bankroll. The general recommendation is to throw in the towel when you are left with fewer than six betting units.
So if you bet $50 per hand, you must ensure you have at least $300 before you continue playing; if you wager $100, you end the session when you are down to less than $600 and so on.
The reason for this is simple – you need enough money to back up any potential splitting and doubling decisions in line with basic strategy. The bottom line is you should never stay at the table if you are so underbanked that you can no longer exercise the optimal playing decisions. Doing the opposite will ultimately cost you money in the long run.